Optics of disordered systems group

A brief introduction to fractional calculus

Disclaimer: what follows assumes familiarity with calculus (in particular with derivatives and integrals). This is also no substitute for a proper textbook, as we will be very hand-weavy and skip a lot of details. If you are looking for a more complete and rigorous introduction to the topic, I suggest you check "Fractional Differential Equations" by I. Podlubny.

The history of fractional derivatives begins together with the history of the much more common integer-order derivatives, and a number of big names in mathematics worked on it over the centuries. Since differentiating twice a function yields the second derivative, the Marquis de l'Hôpital immediately wondered whether it makes sense to think about an operator which, if applied twice, gave the first derivative, i.e. some sort of derivative of order ½. He asked the question to Leibniz in a letter, and Leibniz started working on it. And while he didn't really managed to make sense of it, he developed a product rule that fractional derivatives should have obeyed.
The first one to propose a working definition of fractional derivative was Euler. In modern language, every analytical function can be expressed as a polynomial, and the formula for the derivative of a monomial can be generalized to order α∈ℝ: \[ \partial^n_x x^m = \frac{m!}{(m-n)!} x^{m-n} \rightarrow \partial^{\alpha}_x x^m = \frac{\Gamma(m+1)}{\Gamma(m+1-\alpha)} x^{m-\alpha} \, . \]

This definition of a fractional derivative has many advantages: it is intuitive, it applies to a huge class of useful functions, and it is not difficult to evaluate. It has one big problem: for \( x< 0 \) the result is a complex function even when differentiating polynomials (e.g. \( -1^{0.5} = i \)).

Is there any better way to define a well behaved fractional derivative? An option is to follow the same principle, but starting with another set of functions that are easy to differentiate: complex exponentials (i.e. sinusoidals): \[ \partial^n_x e^{i k x} = (i k)^n e^{i k x} \rightarrow \partial^{\alpha}_x e^{i k x} = (i k)^{\alpha} e^{i k x} \] So if we perform the Fourier transform of a function (i.e. we rewrite it in terms of complex exponentials), we multiply it by \( (ik)^{\alpha}\), and Fourier transform back, we get a fractional derivative (known as the Weyl fractional derivative), which suffer no problem for \( x < 0 \)!

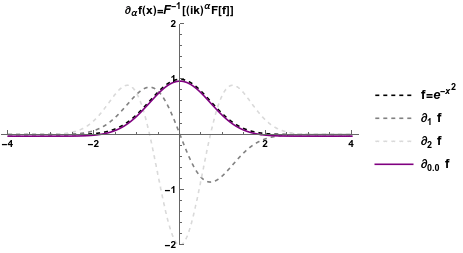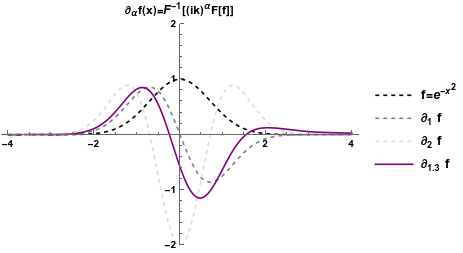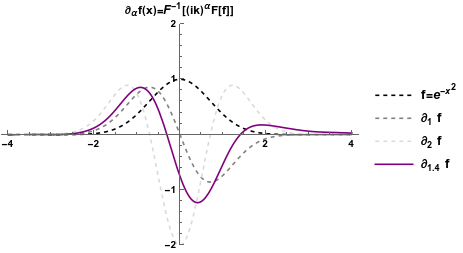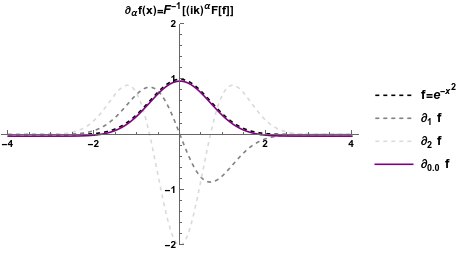
Are we sorted out? Not really.
First of all the Weyl derivative can not be applied to polynomials, which is a problem. Second, this derivative is usually very hard to compute analytically. Also, while both Euler and Weyl definitions agree with integer-order derivatives, the two definitions give different results for fractional orders (e.g. the Euler fractional derivative of an exponential is not another exponential).

A less intuitive approach to defining a fractional derivative is based on Cauchy formula for repeated integrals, which also can be easily generalized to non-integer orders: \[ I_{a+}^n f(x) = \int_a^x \int_a^{x_1} \ldots \int_a^{x_{n-1}} f(x_n) \text{d}x_n\ldots\text{d}x_1 = \frac{1}{(n-1)!} \int_a^x \frac{f(y)}{(x-y)^{1-n}} \text{d}y \rightarrow \] \[ \rightarrow I_{a+}^{\alpha} f(x) = \frac{1}{\Gamma(\alpha)} \int_a^x \frac{f(y)}{(x-y)^{1-\alpha}} \text{d}y \, . \] This gives us a fractional-order integral. So, if we want a derivative of order 0.5, we can just integrate with order 0.5, and then differentiate once (Riemann-Liouville fractional derivative): \[ D_{a+}^{\lceil\alpha\rceil-\alpha} f(x)=\frac{1}{\Gamma(\alpha)} \frac{\partial^{\lceil\alpha\rceil}}{\partial x^{\lceil\alpha\rceil}} \int_a^x \frac{f(y)}{(x-y)^{1-\alpha}} \text{d}y \, . \] It is interesting to notice that this definition has a free parameter a, which we can choose freely. If we set \(a=0\), the Riamann-Loiuville derivative acts on monomials exactly as the Euler derivative did. And if we set \(a=−\infty\) it behaves like the Weyl derivative on sinusoidals. So the Riemann-Liouville derivative is, in a sense, a generalization of both the Euler and the Weyl derivatives, thus unifying them! (It is also not too terrible to evaluate, which is a definitive plus.)
Weirdly, the definition of the Riemann-Liouville derivative is not unique. We could as well have defined it as: \[ D_{b-}^{\lceil\alpha\rceil-\alpha} f(x)=\frac{1}{\Gamma(\alpha)} \frac{\partial^{\lceil\alpha\rceil}}{\partial x^{\lceil\alpha\rceil}} \int_x^b \frac{f(y)}{(x-y)^{1-\alpha}} \text{d}y \, . \] What do you do when you have two equally well behaved but not identical definitions? One option is to take their average:

The only real problem this definition is with Laplace transforms. The formula for the Laplace transform of the fractional derivative, is not much different from the one for integer-order derivatives, but the boundary conditions you need to specify are fractional derivatives. The problem here is that, while integer-order derivatives have a nice Physical interpretation, fractional derivatives don't (and people have tried very hard to come up with a Physical interpretation). So specifying those boundary conditions is also hard.
This can be solved easily, by first doing the integer-order derivative, and then the fractional order integral, which lead to the Caputo fractional derivative, which is (as far as I am aware) the most used definition.

But if fractional derivatives do not have a nice Physical interpretation, are they useful for anything? The point is that while integer-order differential equations tend to give raise to exponentials, fractional order differential eq tend to give rise to power laws. So fractional derivatives tend to be useful every time you need to model stuff with power-law dependencies, or you need something that nicely interpolate between exponentials and polynomials. The example I am most familiar with is anomalous diffusion (either sub or super-diffusion), which are best described in terms of fractional diffusion equations. Other applications include viscoelasticity and electrochemistry.